
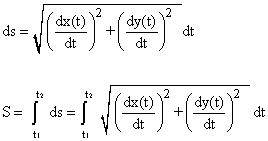
Please e-mail any correspondence to Duane Kouba byĬlicking on the following address heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy. For a circle, the arc length formula is times the radius of a circle. Your comments and suggestions are welcome. Ĭlick HERE to see a detailed solution to problem 12.Ĭlick HERE to return to the original list of various types of calculus problems. $$ ARC = \displaystyle $ on the closed interval $ 1 \le y \le 2 $. The formula for the length of an arc: l 2r (C/360) where, l length r radius C central angle What is an arc measurement The arc measure is a degree measurement that shows the central angle of the arc. It then follows that the total arc length $L$ from $x=a$ to $x=b$ is The arc's length can be calculated with the central angle of the arc and the radius of the circle. Using the Pythagorean Theorem we will assume that We will derive the arc length formula using the differential of arc length, $ ds $, a small change in arc length $s$, and write $ds$ in terms of $dx$, the differential of $x$, and $dy$, the differential of $y$ (See the graph below.). 1) T/F: The integral formula for computing Arc Length was found by first approximating arc length with straight line segments. Consider a graph of a function of unknown length $L$ which can be represented as $ y=f(x) $ for $ a \le x \le b $ or $ x=g(y) $ for $ c \le y \le d $.

In rectangular coordinates, the arc length of a. Let's first begin by finding a general formula for computing arc length. Arc length is the distance between two points along a section of a curve. The function and its derivative must both be continuous on. The following problems involve the computation of arc length of differentiable functions on closed intervals. The length of an arc along a portion of a curve is another application of the definite integral. From this point on we are going to use the following formula for the length of the curve. Arc Length of Differentiable Functions on a Closed IntervalĬOMPUTING THE ARC LENGTH OF A DIFFERENTIABLE FUNCTION ON A CLOSED INTERVAL Instead of having two formulas for the arc length of a function we are going to reduce it, in part, to a single formula.


 0 kommentar(er)
0 kommentar(er)
